本院紹介パンフレット

本院の活動を易しく紹介したパンフレットを作成しました。　パンフレットダウンロード

和算に挑戦してみよう

和算（わさん）とは日本独自に発達した数学のことです。江戸時代には大いに発展し、ヨーロッパの影響を受けずに独自に積分法の発見などがなされました。下記の問題は、パンフレットの中に掲載されていますが、1674年に池田昌意により書かれた『数学乗除往来』という書物に載っている問題をアレンジしたものです。息抜きに挑戦してみましょう。

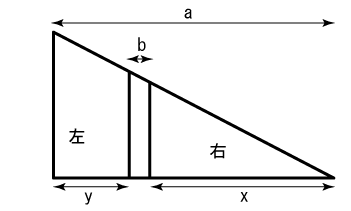
底辺をａとする直角三角形があります。その中に図のように幅ｂの道筋を底辺に垂直に交わるように入れて、右と左の区画に分けます。ここで右と左の区画を同じ面積にしたい場合、底辺にあたるｘとｙの長さはaとbを用いてどのように表されるでしょうか。(出典：池田昌意『数学乗除往来』(1674年)による出題を改変。)

 

解説

この問題の条件には直角三角形の底辺だけが与えられていて、高さに相当するものが与えられていません。これで答が求められるのかどうか不思議に思われたかもしれませんが、後に述べるように、高さの条件はなくとも答を導けます。

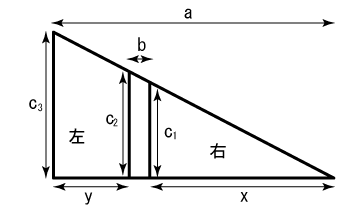
図のように、道幅bの部分の高さをc₁、c₂とし、直角三角形全体の高さをc₃とします。このとき、右と左の面積が等しいという関係から次の式が成り立ちます。

(右の面積＝全体の直角三角形の面積－(右と道の面積)＝左の面積)

・・・・・・①

さらに、相似な直角三角形の間に次の比例式が成り立ちます。

したがって

・・・・・・②

②を①に代入して整理すると、次のxに関する２次方程式が得られます。

 

これを解いて、x > 0より、答は以下に示したものとなります。
また、yは　y = a - b - xによって求められます。

答え